My first encounter with probability came in XI grade and it remained a part of our studies until graduation. I have to admit that probability failed to build any kind of curiosity or interest in me until recently.
When I started learning probability, predicting the probability of equally likely events, like in the case of a coin toss and a throw of dice seemed trivial.
In the course that I am enrolled in currently with the IIT Madras, we have to learn statistics in depth. I heard about the birthday paradox from a class in statistics. Probably, that is the point I started to develop an interest in the subject. It is an interesting concept and hence wanted to share it here.
What is birthday paradox?
It says that in a random group of 23 people, there is a 50% chance that there are two people who share the same date of births.
There are 365 days in a year. To me, it sounded almost impossible to have two people sharing the same date of births in a group of just 23.
So, I turned to my class (coincidentally of strength 23) and found that my classmates Rekha and Divya celebrated birthdays on the 7th of Jan.
I checked with my friend and old roommate Dhanya about her class. She had a class strength of nearly 40. Preetha and Reena from her class celebrated their birthdays on the same day.
I checked with my spouse's young cousin Devika and also with my spouse's friend's wife Dr. Dhanya about their classes. They however don't remember anyone sharing the same birthdays in their classes of smaller sizes.
So, effectively my enquiries gave me a result of 50%
This can be mathematically proved too. I will defer the proof for now and post it under a different blog a bit later.
There are few other notes that I would like to make:
If the size of the random group is 10, the probability of you finding a pair of people who share the same birthday is less and is hardly 11%.
If the size of the random group is 23, the probability of you finding a pair of people who share the same birthday is 50%.
If the size goes up to 40, the probability goes up to 90%.
If the size further goes up, say 60, the probability would shoot up further and would be 99%.
This means that if you have a group of random circle of more than 60 , you finding friends who share the same birthdays in that group is not a coincidence and is bound to happen as per probability!
You may try looking into your facebook or linkedin or on your twitter feed to validate this. Or you may even look within your classmates itself and there is a 50% chance that you will find people sharing the same birthdays if you had a class strength of 23. If the class strength is 40 or more, chances of you finding people share the same birthdays is almost certain!
Programmatically simulating the birthday paradox
Below is a small piece of code written in Python.
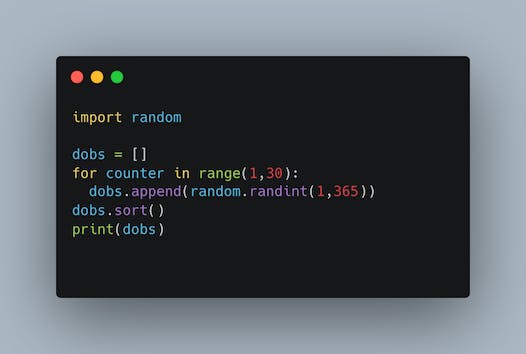
About the code
The above code generates 30 random date of births. The birthday list is then sorted to identify repetitions easily.
It uses the random library in Python and generates 30 ints between 1 and 365. If we assume that 1 corresponds to Jan 1st, 2 corresponds to Jan 2nd and so on, 365 corresponds to Dec 31st.
The result of some runs of this program is pasted below.
Run 1:

Here 131 is repeated. 131 should correspond to May 11th. So, in this group, 2 people shared the same birthday on the 11th of May.
Run 2:

In this run, 206 is repeated. 206 corresponds to 25th of July. That way, in this group, 2 people shared the same birthday on the 25th of July.
Run 3:

Likewise, in this group, there are two people who share the birthday on the 16th of April. (106th day of the year corresponds to 16th April.)
More runs:

Here are the results of the 6 runs I made. The first 3 had repetitions and the last 3 didn't have. Which means the first three groups had people sharing the same birthdays and the last 3 groups didn't have anyone sharing the same birthdays.
If we try it for a group of 60, we can see that, the repetition is almost certain since the probability in that case is 90%.
Probability is sometimes mesmerising!